Next: Der Schutz der galvanischen Up: Der Schutz der Isolationsbarriere Previous: Theoretische Grundlagen magnetischer Kreise

Berechnung eines magnetischen Kreises am Beispiel eines Ferritkernes EF16

Um magnetische Kreise irgendwie rechnerisch auf einfache Weise in den Griff zu bekommen, bedienen wir uns der Analogie zwischen einem elektrischen und einem magnetischen Kreislauf.

Berechnungen in elektrischen Kreisen sind elementar und sind sicher schon jedem Student der Elektrotechnik in den ersten Semestern geläufig.

Bei der Betrachtung magnetischer Zusammenhänge tut man sich damit schon viel schwerer. Berechnungen in der magnetischen Welt sind für den praktizierenden Elektroniker, der sich in aller Regel in elektrischen Kreisen recht gut auskennt, eine allenfalls obskure Sache und entziehen sich sehr oft recht widerspenstig einer halbwegs exakten quantitativen Definition. Allzuoft ist die Konstruktion von z.B. von Übertragern von DC/DC-Konvertern eine Vergehensweise des gezielten Probierens einhergehend mit einer ganzen Portion Erfahrung, oder die Werte für den Aufbau solcher Geräte werden mit Hilfe von Herstellerangaben oder -programmen gefunden. Dagegen ist auch nichts einzuwenden, wenn es nachher funktioniert.

In diesem Aufsatz wollen wir aus der Sichtweise eines Elektronikers, der Tag für Tag in elektronischen Schaltungen zu Hause ist, diese berechnet oder simuliert und damit gut zurecht kommt, uns an magnetische Kreise heranwagen, ohne zu sehr in den Magnetismus einzutauchen. Wir werden versuchen, die magnetischen Grössen und Zusammenhänge auf elektrische Vorgänge zuführen und sie so in ein Korsett zu bringen, das uns erlaubt, die ganze Angelegenheit wie ein elektrischen Stromkreis zu betrachten.

Wir haben die Möglichkeit dadurch, Schaltungssimulationsprogramme wie PSPICE, Spice3f5 usw. , Tabellenkalkulationen auf magnetische Kreise in einfache Weise anzuwenden.

Diese Gedanken finden ihre Realisierung in einem Wirkprinzip zum Schutze der galvanischen Isolation vor dem Durchschmelzen bei DC/DC-Wandlern in Netzteilen, was am Ende eine breiten Raum dieses Aufsatzes einnehmen wird.

Wir berechnen einen magnetischen Kreis an einem Ferritkern der aus zwei Hälften besteht und folgende geometrischen Abmasse besitzt:

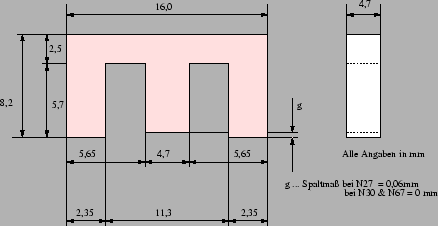
$\resizebox* {0.8\textwidth}{!}{\includegraphics{magnet8.eps}}$

Bild 6: Abmasse des EF16-Ferritkernes

Der Hersteller von solchen Kernen gibt dazu die unterschiedlichsten Parameter der Masse an, wovon für unsere Abschätzung die Anfangspermeabilität µi bei Ta=25°C vorerst interessant ist:

Wir werden uns für zwei Materialien interessieren und wollen uns die Ferritmassen N30 und N27 stellvertretend von der Fa. Siemens Matsushita Components vornehmen:

$\begin{displaymath}\mu _{i}(N30)=4300\end{displaymath}$

$\begin{displaymath}\mu _{i}(N27)=2000\end{displaymath}$

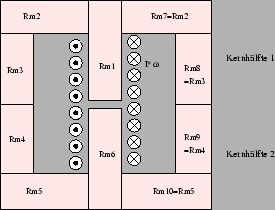
$\resizebox* {0.5\textwidth}{!}{\includegraphics{magnet2.eps}}$

Bild 7: Schematische Zusammensetzung eines magnetischen Systems, dass aus zwei Ferrithälften besteht und zur Vereinfachung in einzelne Segmente zerlegt ist.

Uns sind alle Abmasse des Kernes bekannt, und wir zerlegen unseren Ferritkern zur Vereinfachung in für die Berechnung passende Stücke. Wir gehen auch davon aus, dass an den hochgeschliffenen Flächen zwischen Rm3 und Rm4 sowie zwischen Rm8 und Rm9 kein Luftspalt existiert, was natürlich in der Praxis nicht stimmt, aber zur Vereinfachung einmal angenommen wird. Diese Teile, insgesamt 10 Stück, und der Luftspalt zwischen Rm1und Rm6, falls vorhanden, bilden den magnetischen Gesamtwiderstand Rmg mit einer magnetischen Spannungsquelle MMK = $\Theta =$ I * Wi:

Die Widerstände Rm1, Rm2 , Rm3, Rm7 und Rm8 gehören zur Kernhälfte 1, die Widerstände Rm4, Rm5, Rm6, Rm10 und Rm9 zur Kernhälfte 2.

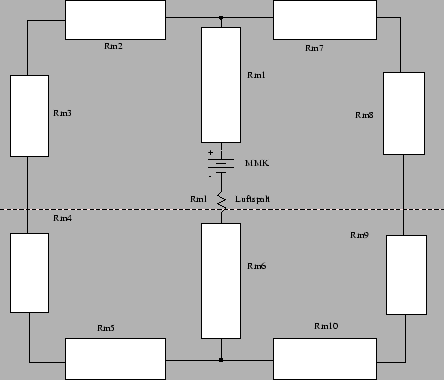
$\resizebox* {0.8\textwidth}{!}{\includegraphics{magnet4.eps}}$

Bild 8: Das Ersatzschaltbild des EF16-Übertragers. Die einzelnen Ferritsegmente werden als magnetische Widerstände betrachtet.

Unser Schaltbild sieht nun wie ein elektrischer Kreis aus, den wir nun wie eben einen solchen berechnen können, also die entsprechenden Ströme (=magnetischen Flüsse $\Phi$ ) und Spannungsabfälle . Dafür müssen wir erst einmal die einzelnen magnetischen Widerstände von Rm1 bis Rm10 und den magnetischen Widerstand des Luftspaltes RmL abschätzen. Bei dieser Berechnung der magnetischen Flüsse vereinfachen wir auch noch, dass ein Grossteil des magnetischen Flusses sich im Ferrit und über den Luftspalt zwischen dem Mittelschenkel abspielt und dass der Luftspalt sehr viel kleiner als die Breite des Mittelschenkels ist (0,06 mm << 4,7mm).

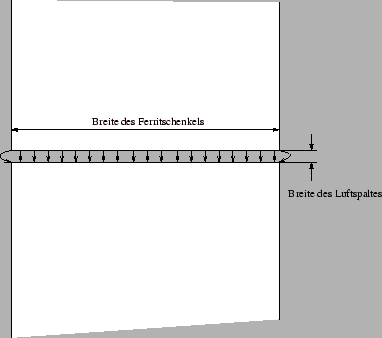
$\resizebox* {0.7\columnwidth}{!}{\includegraphics{magnet9.eps}}$

Bild 9: Nicht ganz masstabsgetreue Darstellung des Luftspaltes im Mittelschenkel des EF15-Kernes

Für die Widerstandsberechnung nehmen wir die Beziehung

$\begin{displaymath}R_{mj}=\frac{l_{j}}{\mu _{j}*Aj}=\frac{l_{j}}{\mu _{0}*\mu _{rj}*A_{j}}=\frac{1}{\mu _{rj}}*\frac{lj}{\mu _{0}*A_{j}}\end{displaymath}$

zu Hilfe und fangen mit Rm1 an:

Der Abschnitt Rm1 gehört zur Kernhälfte 1 mit dem Material N30 mit folgenden Parametern:

µr = 4300

l = 8,2mm = 8,2 *10 $^{-3}$ m

A = 4,7mm * 4.7 mm = 4,7 * 10 $^{-3}$ * 4,7 * 10 $^{-3}$ m $^{2}$ = 22,09 * 10 $^{-6}$ m $^{2}$

$\begin{displaymath}R_{m1}=\frac{1}{4300}*\frac{8,2*10^{-3}m}{1,256*10^{-6}\frac{Vs}{Am}*22,09*10^{-6}m^{2}}\end{displaymath}$

$\begin{displaymath}R_{m1}=6,873*10^{4}\frac{A}{Vs}=68,73k\end{displaymath}$

Diese Rechnung setzt sich nun für jeden Abschnitt im magnetischen Kreis fort, dabei sind die Materialkonstanten für den jeweiligen eingesetzten Ferrit und für den Luftspalt zu beachten. Wir erhalten für jeden Abschnitt einen magnetischen Widerstand Rmj. Bemerkenswert ist, dass der 0,06mm breite Luftspalt den weitausgrössten magnetischen Widerstand von 2162 k $\frac{A}{Vs}$ aufweisst.

Abschnitt	magnetische Widerstand in k $\frac{A}{Vs}$
Rm1	68,73
Rm2	89,03
Rm3	95,55
Rm4	205,44
Rm5	191,42
Rm6	147,77
Rm7	89,03
Rm8	95,55
Rm9	205,44
Rm10	191,42
RmL	2162,55

Tabelle 1: Errechnete Magnetische Widerstände eines jedes Segmentes der beiden Ferrithälften aus Bild 7 und 8 bei einer Temperatur von Ta=25°C

Der Gesamtwiderstand dieses magnetischen Kreises Rmg ergibt sich aus Bild 8:

$\begin{displaymath}R_{mg}=R_{mL}+R_{m1}+R_{m6}+\frac{R_{m2}+R_{m3}+R_{m4}+R_{m5}}{2}\end{displaymath}$

$\begin{displaymath}R_{mg}=2669,77k\end{displaymath}$

Der magnetische Widerstand, den eine magnetische-motorische Kraft $\Theta =I*Wi$ für einen EF16-Kern aus einer Hälfte N27 und N30 mit einem Luftspalt von 0,06mm beträgt 2669,77k $\frac{A}{Vs}.$ Wenn jetzt auf diesen Kernverband eine Wicklung aus Kupferdraht mit z.B. Wi=40 Windungen aufgetragen wird und durch diese Spule ein Strom I von 0,1 A geschickt wird, dann errechnet sich ein magnetischer Fluss:

$\begin{displaymath}\Phi _{g}=\frac{MMK}{R_{mg}}=\frac{\Theta }{R_{mg}}=\frac{I*......9,77k\frac{A}{Vs}}=\frac{4AWi}{2669,77\frac{kA}{Vs}}=1.50\mu Vs\end{displaymath}$

Die MMK wird bei unseren Konstruktionen auf den Mittelschenkel angesetzt, der Fluss findet seinen Antrieb im Mittelschenkel und breitet sich über die beiden Seitenschenkel aus. Aufgrund der Symmetrie dieser beiden Seitenschenkel (gleiche magnetische Widerstände) teilt sich dieser in zwei gleichgrosse Hälften auf:

$\begin{displaymath}\Phi _{g}=\Phi _{1}+\Phi _{2}=\frac{\Phi _{g}}{2}+\frac{\Phi _{g}}{2}\end{displaymath}$

Die magnetischen Grössen lassen sich auf elektrische übertragen:

Die magnetische Spannunngsquelle $\Theta =I*Wi$ in A_windungen entspricht der Spannungsquelle U in V. Der magnetische Widerstand Rm in $\frac{A}{Vs}$ entspricht dem ohmschen Widerstand R in $\Omega .$ Der magnetische Fluss $\Phi$ in µVs entspricht dem elektrischen Strom I in µA.

Daraus kann ein elektrischer Stromkreis gebildet werden, der in seiner Zusammenschaltung seiner ``Bauelemente'' , dem des magnetischen Kreises entspricht und mit einem Schaltungsanalyseprogramm wie PSPICE simuliert werden kann. In unserem Fall wurde der magnetische Fluss jeweils einmal ermittelt als der N30-Kern noch nicht die Curietemperatur erreicht hat und dann noch einmal, wenn die N30-Kernhälfte 130°C überschritten hat und die relative Permeabilität gegen 1 geht.

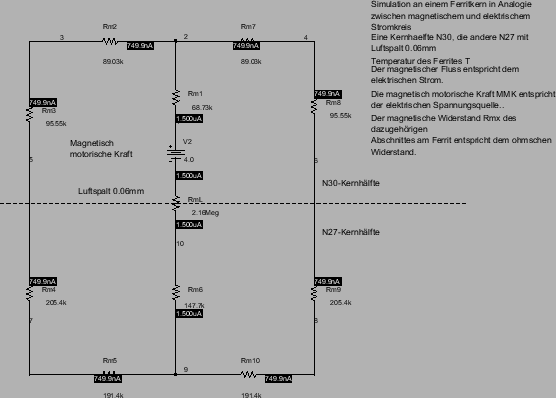
$\resizebox* {1\textwidth}{!}{\rotatebox{270}{\includegraphics{spice1o.eps}}}$

Bild 10: Schaltbild in PSPICE für den EF16-Übertrager mit 40 Windungen und einem Spulenstrom von 0,1A bei einer Temperatur von Ta=25°C

Überschreitet die Temperatur die Curietemperatur des N30-Kernes dann werden die magnetischen Widerstände Rm1, Rm2 , Rm3, Rm7 und Rm8 schlagartig grösser, weil

$\begin{displaymath}\mu _{i}(N30)=4300\end{displaymath}$ zu

$\begin{displaymath}\mu _{i}(N30)=1\end{displaymath}$ wird.

Abschnitt	magnetischer Widerstand in k $\frac{A}{Vs}$
Rm1	295539
Rm2	382829
Rm3	410865
Rm4	205,44
Rm5	191,42
Rm6	147,77
Rm7	382829
Rm8	410865
Rm9	205,44
Rm10	191,42
RmL	2162,55

Tabelle 2: Errechnete Magnetische Widerstände eines jedes Segmentes der beiden Ferrithälften aus Bild 7 und 8 bei einer Temperatur von Ta>130°C

Der gesamte magnetische Widerstand erhöht sich gravierend

$\begin{displaymath}R_{mg}=R_{mL}+R_{m1}+R_{m6}+\frac{R_{m2}+R_{m3}+R_{m4}+R_{m5}}{2}\end{displaymath}$

$\begin{displaymath}R_{mg}=695Meg\frac{A}{Vs}\end{displaymath}$

und verringert der magnetischen Fluss :

$\begin{displaymath}\Phi _{g}=\frac{MMK}{R_{mg}}=\frac{\Theta }{R_{mg}}=\frac{I*......Meg\frac{A}{Vs}}=\frac{4,0AWi}{695Meg\frac{A}{Vs}}=0,0057\mu Vs\end{displaymath}$

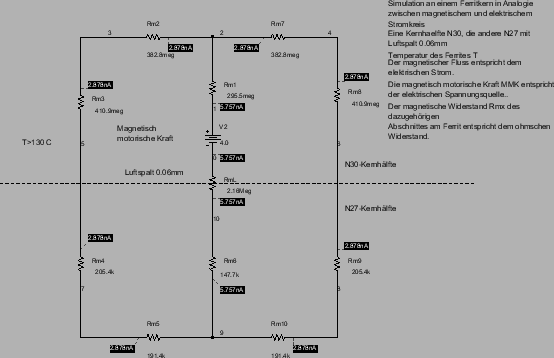
$\resizebox* {1\textwidth}{!}{\rotatebox{270}{\includegraphics{spice2.eps}}}$

Bild 11: Schaltbild in PSPICE für den EF16-Übertrager mit 40 Windungen und einem Spulenstrom von 0,1A bei einer Temperatur von Ta>130°C

Der magnetische Fluss im Kern bricht bei der einer Temperatur oberhalb von T > 130°C zusammen.

Mit diesem magnetischen Modell lassen sich unter Einbindung von mathematischen Funktionen in PSPICE Flussdichten B, Sättigung Bs, induzierte Spannungen U=-Wi* $\frac{d\Phi }{dt}$ , Induktivitäten L= $\frac{Wi^{2}}{R_{m}}$ berechnen, wobei die MMK eine beliebige Kurvenform in PSPICE annehmen kann (Sinus, Rechteck, Pulse usw.) und auch bei unterschiedlichen Temperaturen betrachtet werden kann.

Das Modell lässt sich noch verfeinern, wenn der zugegeben kleine Luftspalt an den beiden geschliffenen Flächen zwischen Rm3 und Rm4 sowie zwischen Rm8 und Rm9 beachtet wird. Durch diese erhöht sich der magnetische Widerstand um einige Prozent, je nach dem wie gut man den Schliff als fein genug annimmt ( 1 bis 3 µm) und damit verringert sich auch die Induktivität.

Die Praxistauglichkeit kann dadurch erweitert werden, aber für Abschätzungen für DC/DC-Berechnungen reicht meist obiges Modell nach unseren Erfahrungen aus:

Windungen auf EF16-Kern	errechnete Induktivität	gemessene Induktivität
(N30,N27,0.06mm Spalt)	aus $L=\frac{Wi^{2}}{R_{m}}$ in µH	in µH
10	37	31
20	149	124
30	337	289
40	599	520
50	936	834

Tabelle 3: Vergleich zwischen der aus dem Gesamtmagnetischen Widerstand Rm errechneten und gemessenen Induktivität L einer unterschiedlich bewickelten Spule. Nicht berücksichtigt sind die magnetischen Widerstände der geschliffenen Flächen

Aus der Tabelle 3 ist ersichtlich, dass eine Differenz zwischen errechneteter und gemessener Induktivität auftritt, die sich u.a. aus aus der Tatsache ableiten lässt, dass die beiden magnetischen Widerstände der geschliffenen Ferritflächen sowie Nebenflüsse über die Luft nicht einbezogen wurden.

Next: Der Schutz der galvanischen Up: Der Schutz der Isolationsbarriere Previous: Theoretische Grundlagen magnetischer Kreise

dietmar berndt
2001-07-01